What does optimization mean?
It refers to maximizing some outcome or minimizing some loss under constrained conditions. For example, consider the problem of optimizing the route from point A to point B.
Intuitively, it is evident that connecting point A to point B by a straight line will minimize the distance.
In reality, the road is a constraint, and it is not possible to go in a straight line.
Thus, there is usually a constraint when it comes to optimization.
Optimality for a shift work schedule
There are also constraints in the shift work schedule. You could say that it is full of constraints. Even in such a situation, there are many things to consider, such as assigning the necessary number of night shift workers, taking into account the skill level of night shift workers, prohibiting pairings, taking care of the uneven number of night shifts among staff members, avoiding night shift concentration during specific periods, taking care of staff quality of life, and so on. There are so many things to consider.
Even more troubling in a shift work schedule is that each chief’s definition of optimal is different. For example, in pair constraints , some managers use a lot of pair prohibitions, while others do not, even in the same workplace. What is optimal is different from one master manager to another.
Leave the boring stuff to the optimization solvers.
On the other hand, there are dedicated optimization engines called optimization solvers worldwide (both commercial and non-commercial).
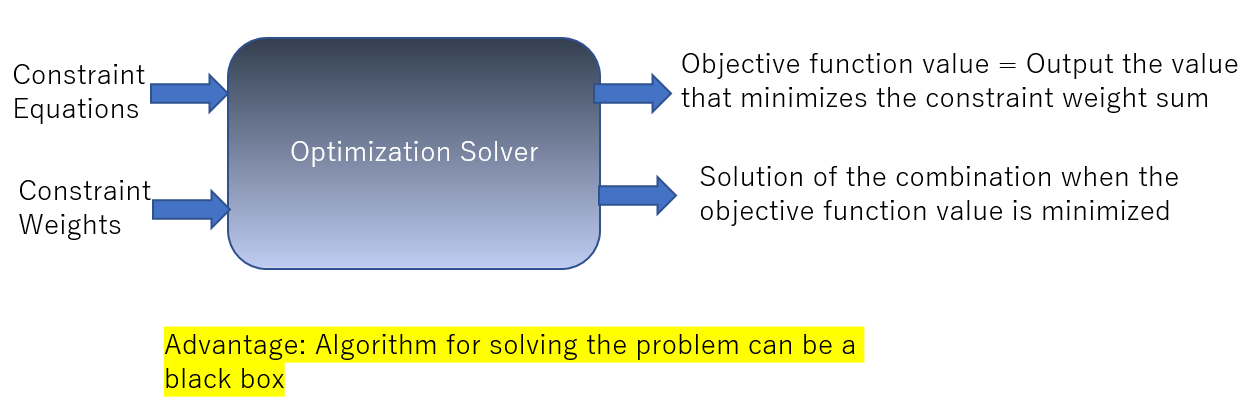
If you enter the constraint and the violation weights of the constraint, it will give you the answer for the combination that minimizes the total violation weight. Once you put it into a formula, it no longer has anything to do with shift work schedules. It becomes a purely mathematical problem. The sum of the total violation weights is called the “objective function value” in academic terms.
The optimization solver requires the input of a formula. Still, for now, regarding mathematical optimization, once the formula is determined, the optimized objective function value will always be the same, regardless of the manufacturer.
The hard part is proving that it is optimal.
By the way, when we say, “The answer to this combination is optimal,” how can we say it is optimal?
In other words, how can we say that a better answer does not exist?
Proving that it does not is much more difficult than discovering that it does. Optimization solvers can do that tedious and challenging thing for you.
Mathematical optimization answer is not always the optimal solution to a shift work schedule.
The difficulty of an automatic shift work schedule increases with scale
, a benchmark test is a mathematical optimum. For the same formula, i.e., the same instance (project), the optimal value is the same, even if the manufacturer is different.
Since the values are the same, there can be competition on how to solve the problem (called an algorithm). The algorithm is not essential for the user as long as the latest and best-performing solver is always available.
But the real problem is that it may not fit the human expectation of what is optimal.
Human feelings cannot be expressed by a linear sum
The cause of this is the linear addition at the heart of this modeling. The weights of violations are expressed by simple addition. We have adopted this method because there is no way to convey feelings to the computer in a simplified manner.
Optimal solution for a shift work schedule is beyond the mathematically optimal solution.
So, as the next best solution, we will first solve a mathematically optimal solution. If it is not different for you, then we are done.
If you feel something different, and there is any discrepancy with what you are looking for, you must readjust the weights. This work is called finding the trade-off point
.

