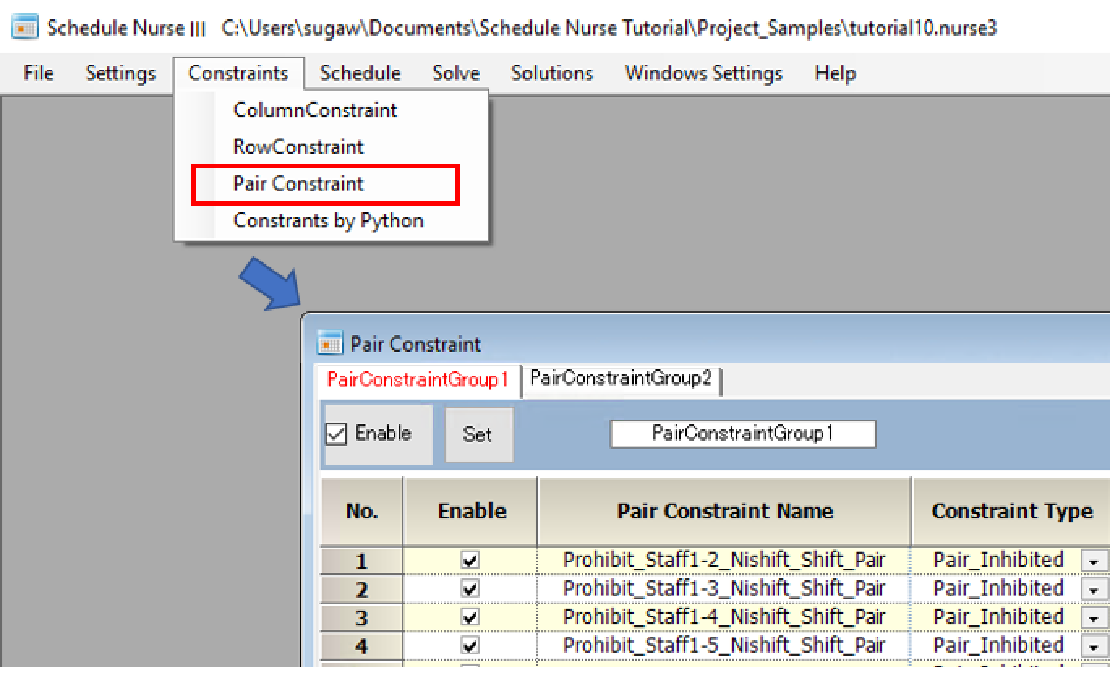
Types of constraints
There are two types of constraints: “Pair_Inhibited” and “If(A)_Then_B”.
“Pair_Inhibited” is a constraint that prohibits Mr. A from working with Mr. B. For example, if they work the same shift, they are prohibited from working that shift.)
When constraining by individual name, the operator “Or” or “And” can be used either way.
Fields that must be set
■Enable Check Box: If not checked, the constraint will be ignored.
■Set Button: After any changes are made, they will not be reflected until you click the set button.
■Except for “Soft Level” and “Day Offset”, all fields must be filled.
■Constraint Type: Specify either “Pair_Inhibited” or “If(A)_Then_B”.
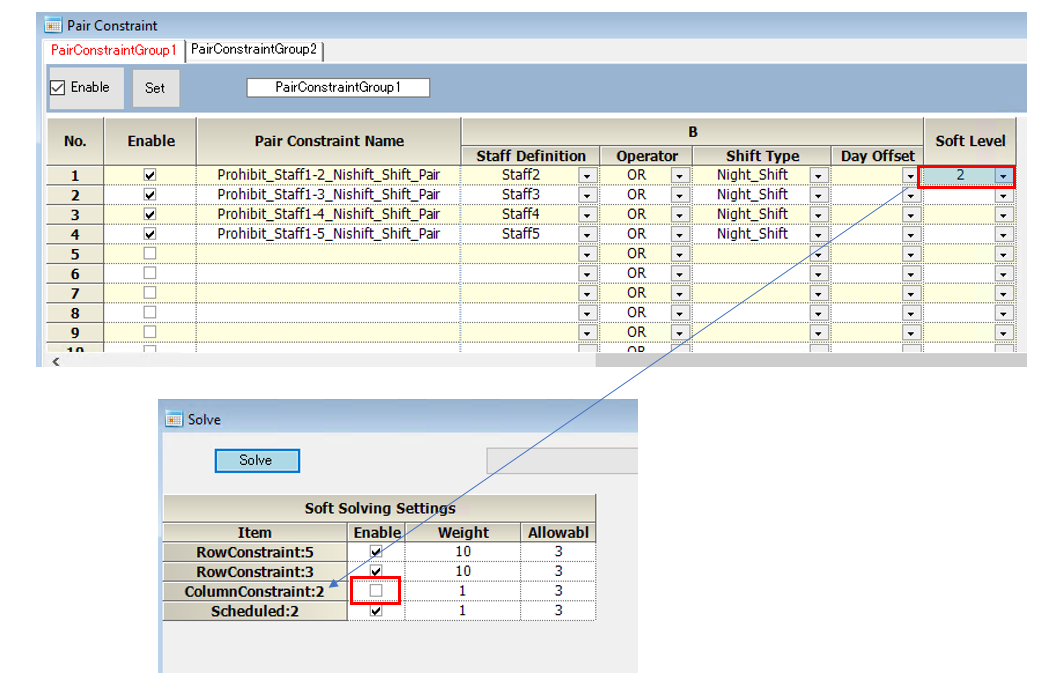
■If any of 1 to 7 is listed for the soft level, the constraint becomes a soft constraint; if not listed, the constraint is a hard constraint.
Soft Constraint
Check Enable Box at the “Column Constraint:“s level, as it is displayed as a column constraint level.
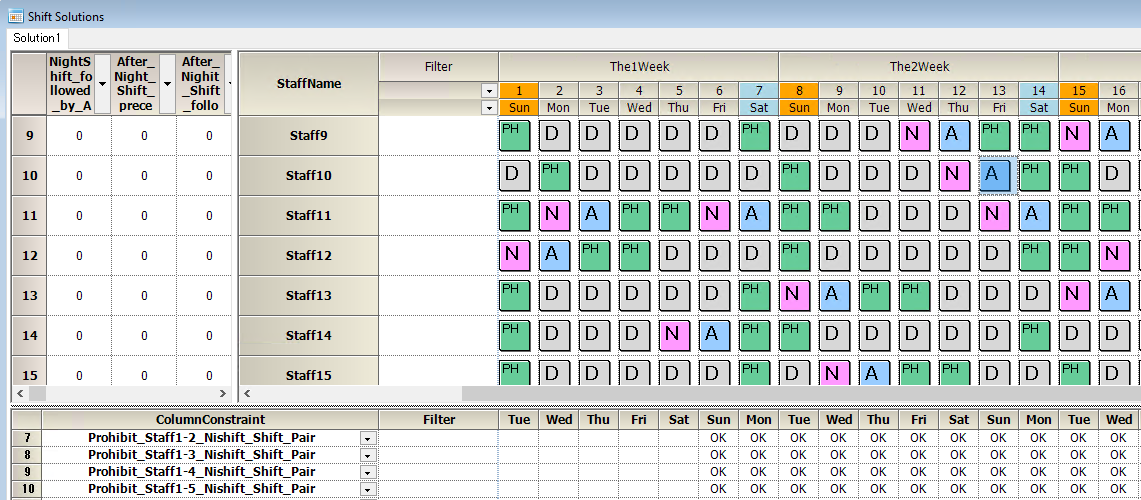
Pair solution display
OK/NG is displayed in the column constraint result section.
If A then B
If A is true, then B must also be true; if A is not true, then B is not constrained in any way.

■ operator <=0 in the above example. If we write the “Or” and “And” operators in this notation, we get the following
“Or” → >=1
“And” →>= all the staff concerned
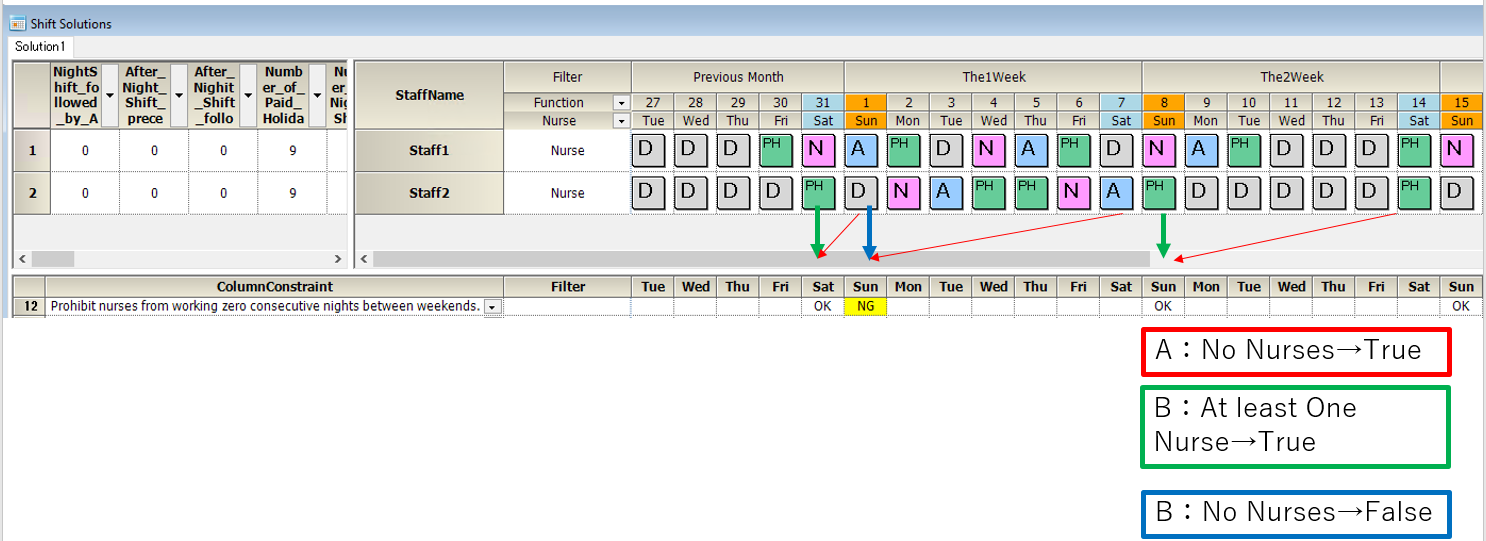
■Day offset: This is the Day offset of B to A. The example above illustrates.
The “weekend” definition for this project is Saturday and Sunday. As a set, from the last month section
Weekend=Saturday, Sunday, Saturday, Sunday…
The set will be “Saturday, Sunday, Saturday, Sunday…”. If A was true on 08 (Sun) when the day offset is -1, then B must be true one day earlier on 07 (Sat).
If A was true on (Sat) 7h, then B must be true one day earlier on 01(Sun).
■Solution display is done only when A is true. Its Day is the Day of B
.
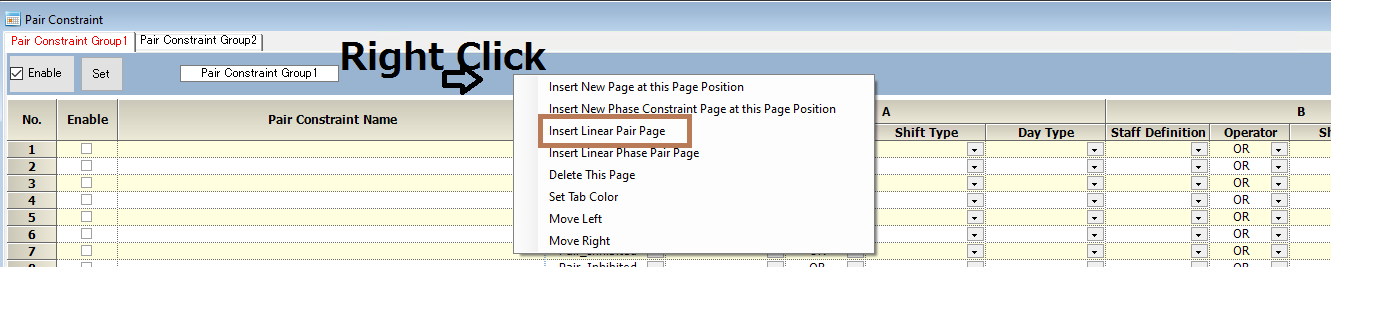
Linear Pair Constraints
By right-clicking on the blue part in the figure below, a menu will appear, from which you can insert a linear pair constraint.
This is a constraint based on mathematical expression.
CoefficientA Operator CoefficientB + offset
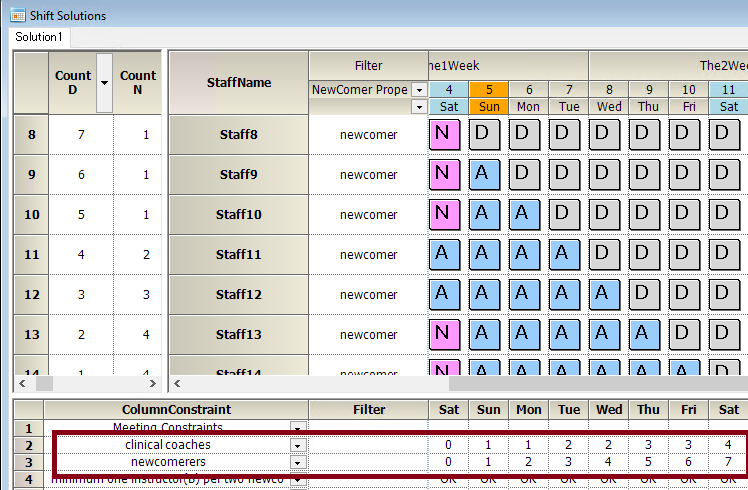
Example of minimum one instructor(B) per two newcomers (A)
Suppose we want to assign a minimum of one instructor (B) per two newcomers (A).
| Newcomers(A) | Minimum Number of instructors(B) |
|---|---|
| 0 | 0 |
| 2 | 1 |
| 4 | 2 |
| 6 | 3 |
This relation can be expressed by the following equation.
A<=2*B

Note the eqation above results the following table.
| Newcomers(A) | Minimum Number of instructors(B) |
|---|---|
| 1 | 1 |
| 3 | 2 |
| 5 | 3 |
| 7 | 4 |
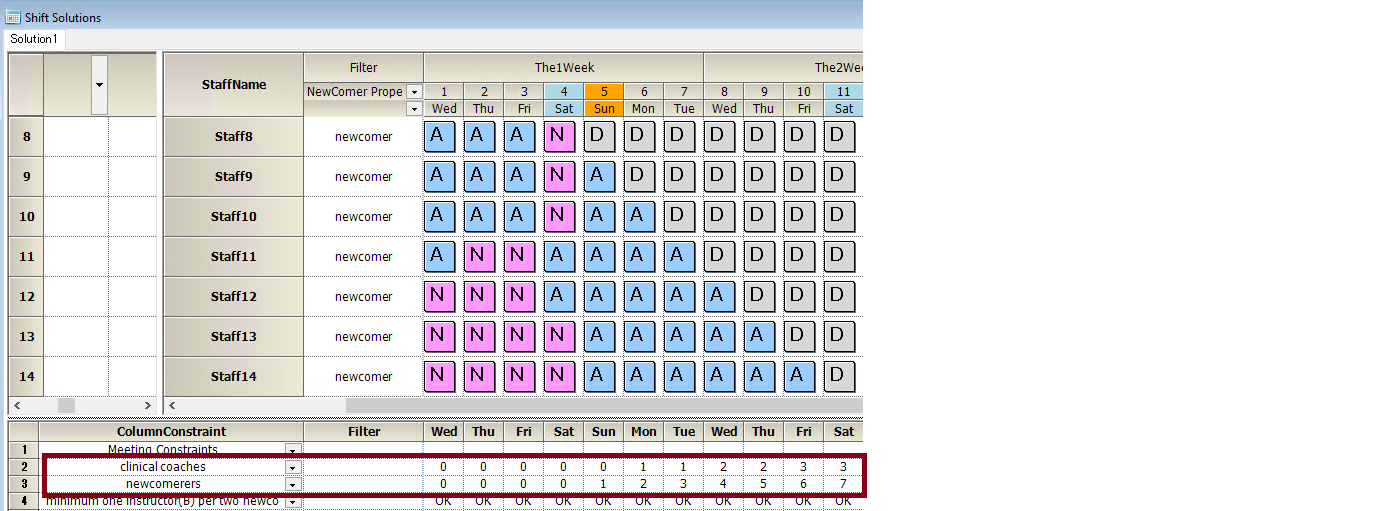
If we want to assign at least one instructor per 3 newcomers like abve, we apply the follwoing equation.
A<=2*B+1
| Newcomers(A) | Minimum Number of instructors(B) |
|---|---|
| 1 | 0 |
| 3 | 1 |
| 5 | 2 |
| 7 | 3 |
Example of Meeting constraints
A*Number of B participants<=B
If the number of participants in the B set is set to BFULL, maintenance of this constraint is not required even if the number of meeting participants, members, etc. change. (AFULL works in the same way.)
In the following example, a conference shift is assigned only to the head nurse.
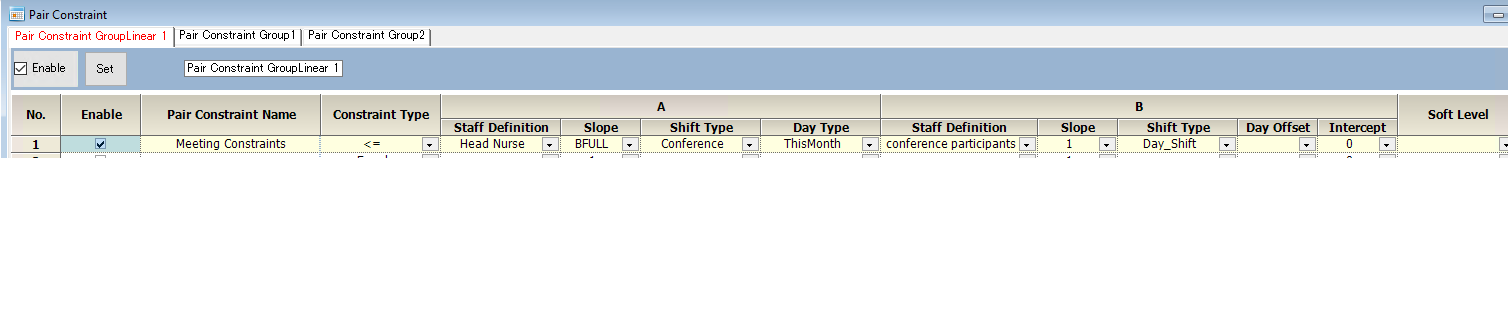
Apart from this constraint, a row constraint is required to describe how many of these conference shifts are in a month.
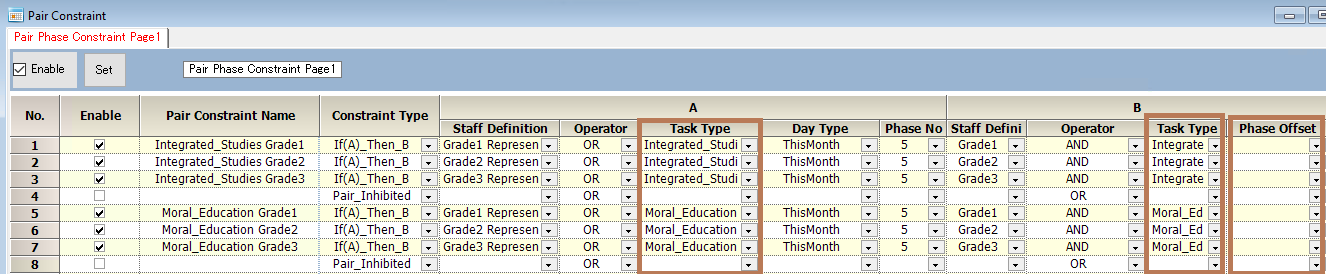
Phase pair constraints
Right-click on the blue section in the diagram below to open the menu and insert phase page.
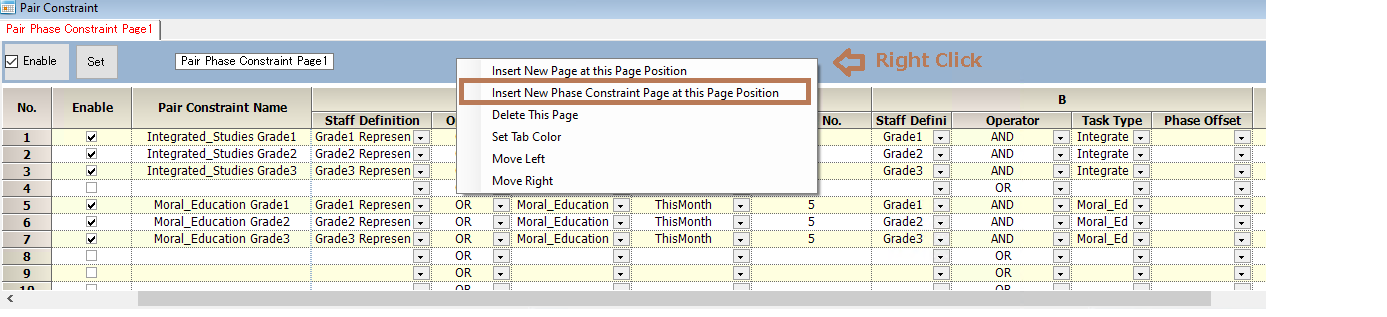
■ Either or both of Shift A or Task A must be described.
■ Either or both of Shift B or Task B must be described.
■Use a task or task set instead of a shift.
■Phase No. must be specified.
■Phase offset is optional. If not specified, it is 0.
■B phase is calculated as follows: B phase = A phase + phase offset. The day is calculated in the range of the set on Day Type.
E.g. A day = Day Type[ADay],APhase=5 phase_offset=-6 when Phase number is 6, BPhase=5 B day = Day Type [ADAY-1]