The above figure shows the last state of the previous
; there was no solution.
The reason for this is that under the condition of absolute adherence to all constraints, a contradiction occurred.
Constraints that adhere to these are called hard constraints. All the constraints we have seen so far are hard.
On the other hand, the constraints that are not adhered to, but are adhered to as much as possible, are called soft constraints.
Namely, there are two types of constraints: hard and soft. If it is not a hard constraint,
it is a soft constraint, and if it is not a soft constraint, it is a hard constraint.
Soft Constraint
Let’s look at the previous error location as a soft constraint and see how it works.
Set the number to the right of the number of times entered, the soft level number to 1. (You can select from 1-7.) When this number is marked, it is a soft constraint. It is a hard constraint if the soft level field is left blank.
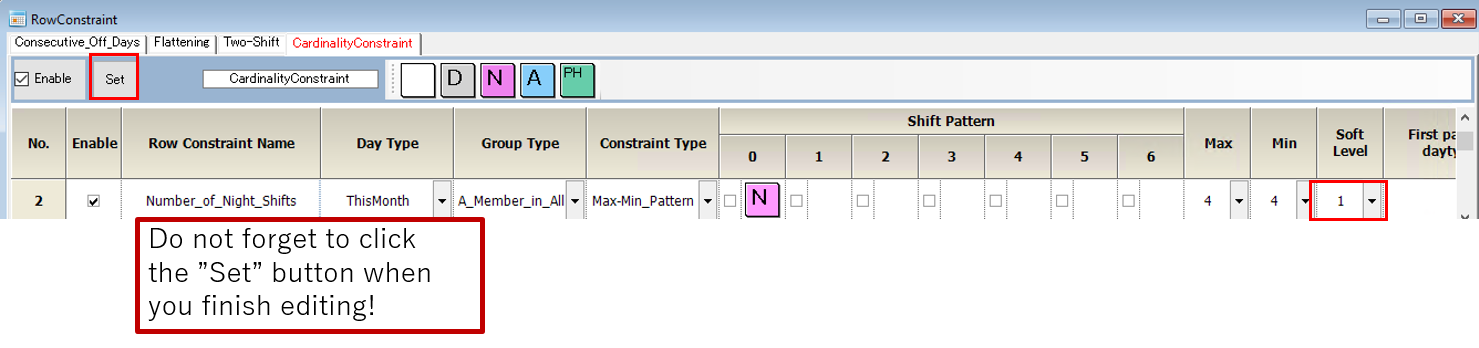
Then on the table below, a line appears that says line RowConstraint:1. We check the box below and solve it.
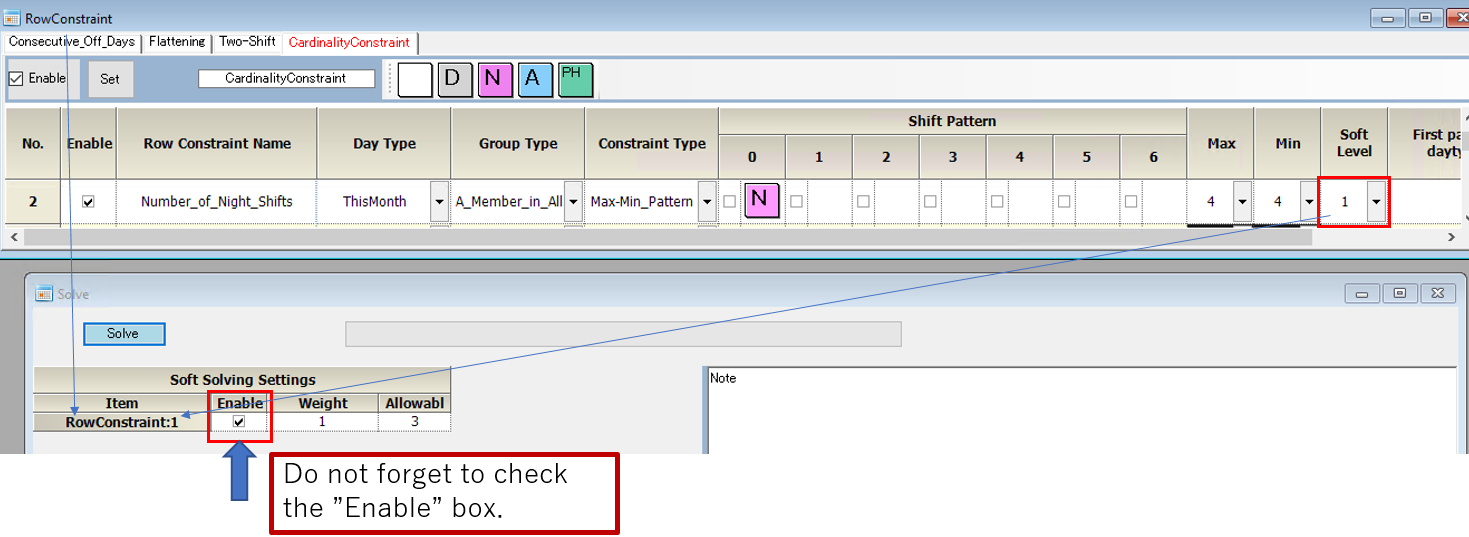
The result is shown in the following screen. The red boxed area is a summary of the errors.
It shows that there are 12 errors with a weight of 1.
The “weight” refers to the priority level. A relatively light weight means a low priority, while a heavyweight means a relatively high priority.
The weight is specified in the table directly below the “Solve” button. Right now, the weight is 1, but since there are no other types of weights, it does not mean much in absolute value since there is nothing else to compare it to.
Deviation of cardinality constraints
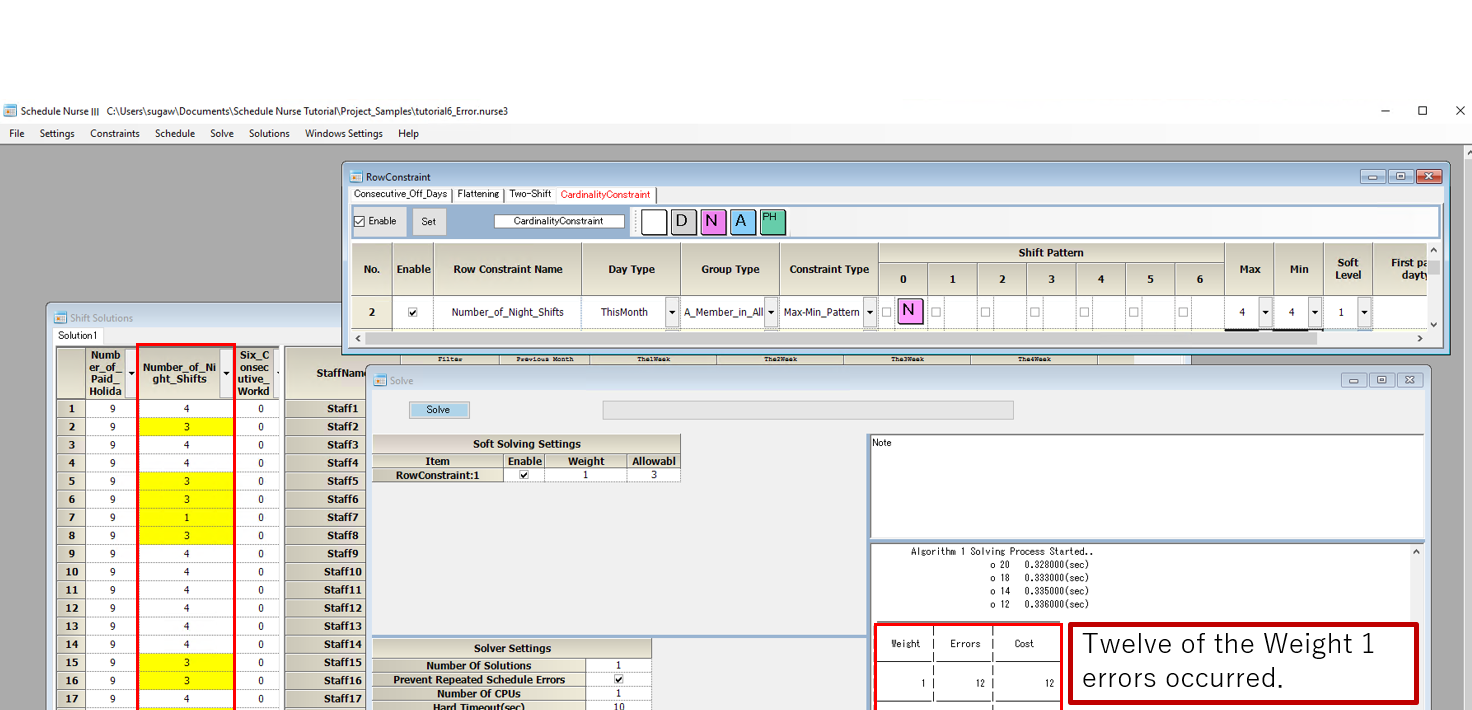
Please see the solution; the marked yellow areas are the error locations.
There are eight places in total. We mentioned earlier that there are 12 errors.
However, there are only eight error locations.
We count one deviation as one error. Then, from the top, (4-3)+(4-3)+(4-3)+(4-1)+(4-3)+(4-3)+(4-3)+(4-3)+(4-3)+(4-1)=12 errors.
Fixing deviation on cardinlality constraints
Ideally, the number of night shifts should be 4, but in the real-world solution, we see that they are widely distributed, ranging from 1 to 4.
(In this example, this is just how it happened, but different PCs have different ways of doing things.)
The deviation is, at most three, unfair from the viewpoint of zero deviated staff, and we want to do something about it.
Therefore, we want to reduce the deviation.
“Allowable Errors” is the allowable deviation of the cardinality constraint. The “Allowable Errors”, which used to be 3, is now 1, and we Solve again.
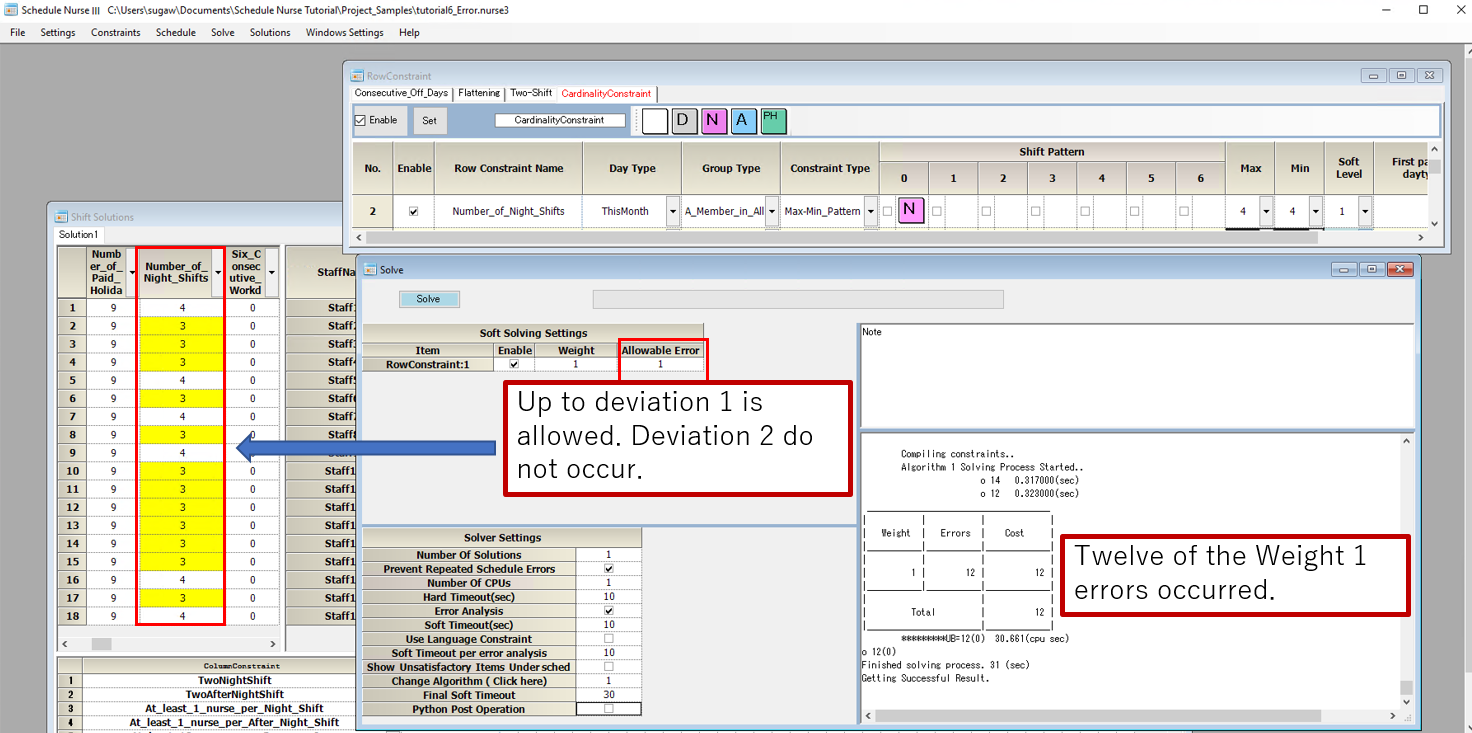
Then, the deviation of the solution is also within 1, and we have achieved the maximum physically possible fair work.
(We had no solution with a zero deviation in previous chapter
as hard constraint.

