最適化の意味
制約のある条件下で、何らかの成果を最大、または損失を最小にすることをいいます。例えば、地点Aから地点Bに行くルートを最適化する、という問題を考えましょう。
直観的には、地点Aと地点Bを直線で結べば、最小距離になるのは、明らかです。
現実には、道という制約があり、直線では行くことはできません。
このように、最適化という場合、そこに制約があるのが普通です。
シフト勤務表にとっての最適
シフト勤務表においても制約があります。むしろ制約だらけ、と言ってもよいでしょう。そういった中にあっても、必要な夜勤人数を配置したり、夜勤のスキルを習熟度を考慮して、ペア禁止を設けたりする一方で、各スタッフ間の夜勤数に偏りに気を配ったり、特定期間に夜勤が集中しないようにしたり、スタッフのQOLに気を配ったり、本当に考慮することは、沢山あります。
シフト勤務表においてさらに悩ましいのは、最適の定義が各師長で、異なることです。例えば、ペア制約 で、同じ職場でも、ペア禁止を多用する師長さんもいれば、そうでない師長さんもいらっしゃいます。何が最適か?が師長さんで異なるのです。
面倒なことは、最適化ソルバに任せる
一方、世の中には、最適化ソルバという最適化専用エンジンが存在します。(商用・非商用、両方存在します)
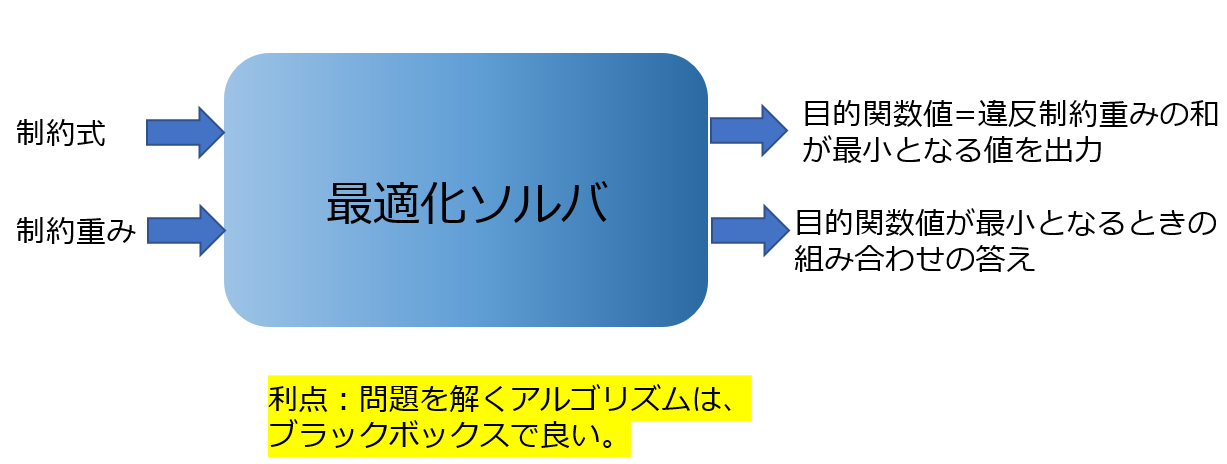
制約と制約の違反度合いの重みを入力すると、トータルの違反重みを最小にする組み合わせの答えを出してくれます。数式にしてしまえば、シフト勤務表とかもはや関係ありません。純粋な数学問題となります。トータルの違反重みの和を学術用語で、「目的関数値」と言います。
最適化ソルバには、数式を入力することが必要なのですが、とりあえず、数理的な最適化に関しては、数式が決まれば、最適化した目的関数値はメーカによらず、常に同じ値となります。
難しいのは最適である証明
ところで、「この組み合わせの答えは、最適である」と言ったとき、どうしてそれが最適であると言えるのでしょうか?
言い換えれば、それよりも良い答えは、存在しない、ということを何故言い切れるのでしょうか?
ないことを証明するのは、あることを発見するよりもずっと難しいことです。最適化ソルバは、そんな面倒で難しいこともやってくれます。
数理的な最適化の答えが、シフト勤務表の最適解とは限らない
自動シフト勤務表の難易度は規模に応じて上がる
で述べた通り、ベンチマークテストというのは、数理的な最適になります。同じ数式、つまり同じインスタンス(プロジェクト)であれば、メーカが違っても最適値は、同じです。
同じ値になるから、どのような方法で解くか(アルゴリズムと言います)競争が出来るのです。利用者にとっては、アルゴリズムは、どうでもよく、常に最新の性能の良いソルバを取り替えれば、よいことになります。
しかし、人間の求める最適の期待値とフィットしないことが現実問題としてありえます。
人の気持ちは足し算では表せない
この原因は、このモデル化の根幹にある足し算です。違反の重みを単純な足し算で表現しています。このような方法を採ったのは、この方法以外に、簡易的にコンピュータに気持ちを伝える手段がないからです。
シフト勤務表の最適解は、数理的最適解の先にある
そこで、次善の策として、まずは、数理的最適解を求めることにします。違和感がなければ、それで終了です。
何か違うな? と、自身の求めるところと違和感があった場合は、重みを再調整する作業が必要となります。この作業は、一般には、トレードオフ点を見つける
作業です。

