良いと思います。
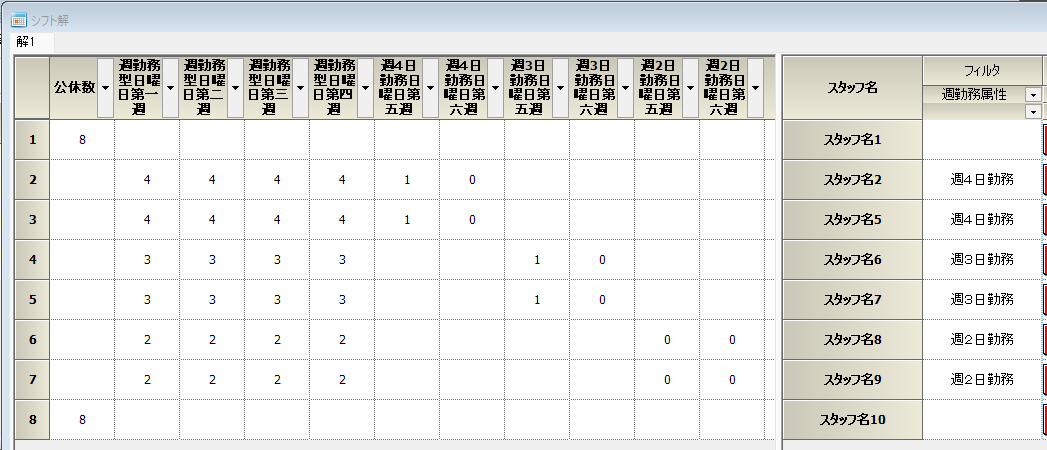
解もちゃんと4回づつになっていました。上のように、マウスホイールボタンを押して、各集合が意図通りになっていることを確認すると間違いなく制約できます。
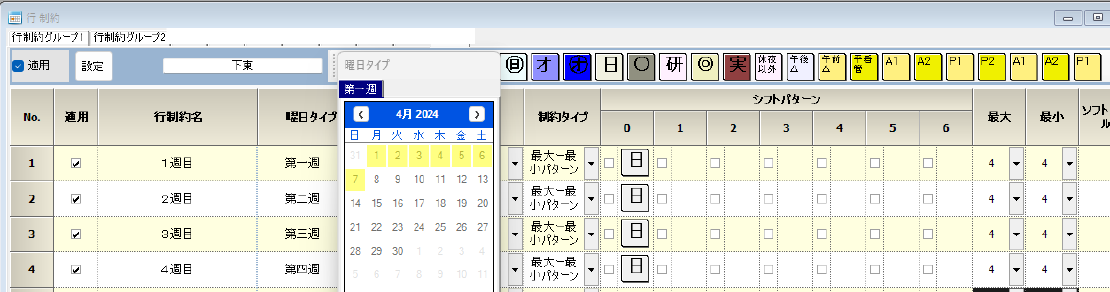
月始まりの一週間ベースで行うやり方は、この方式で良いと思います。 端数の第5週は手入力にしてもよいでしょう。
「日曜日始まりの一週間」を先月からの1週間も見て継続する場合
月始まり基準ではなく、曜日基準で行うには、一般的にはPythonで書く必要があります。
しかし、先月区間6日間に限定 の場合、Pythonを使わなくても可能です。
先月が6日分あるとすると、以下の色部分に最初の日曜日がどのパターンにも一個だけ含まれます。
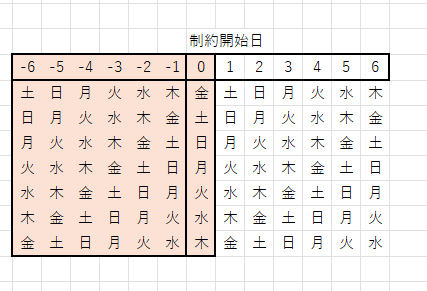
これを利用して、次のように曜日集合を構築出来ます。
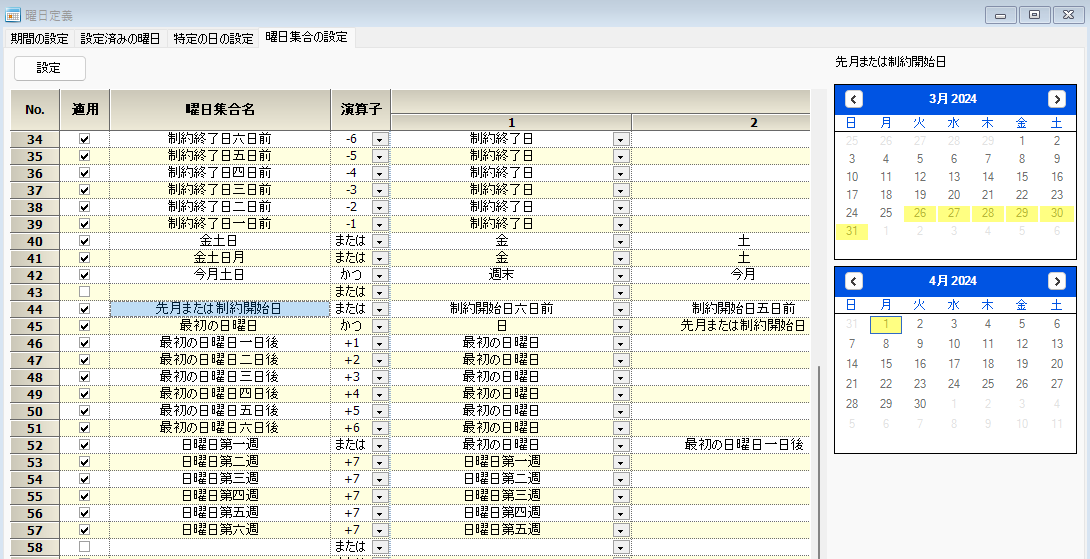
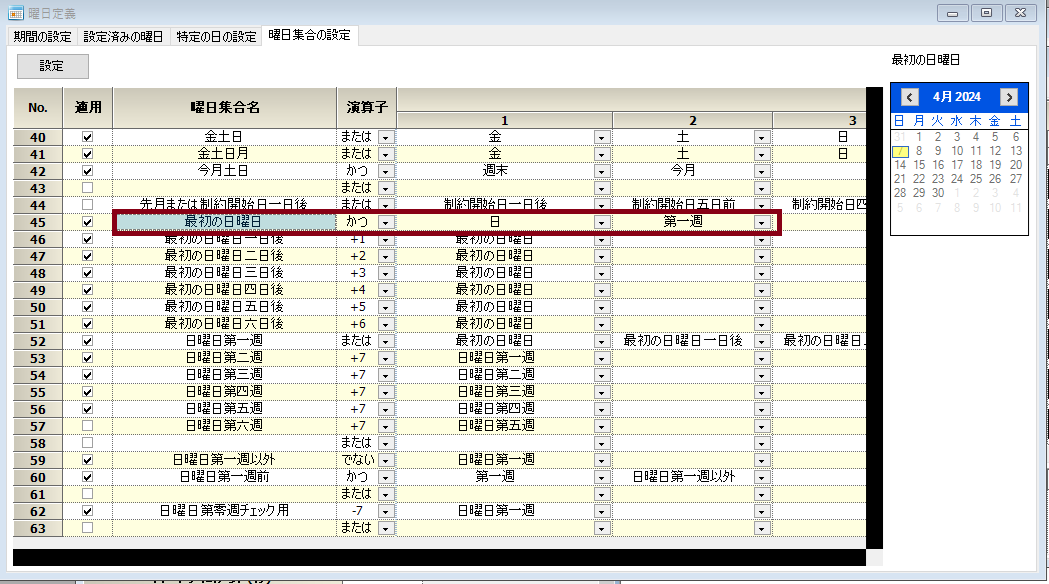
最初の日曜日の定義です。
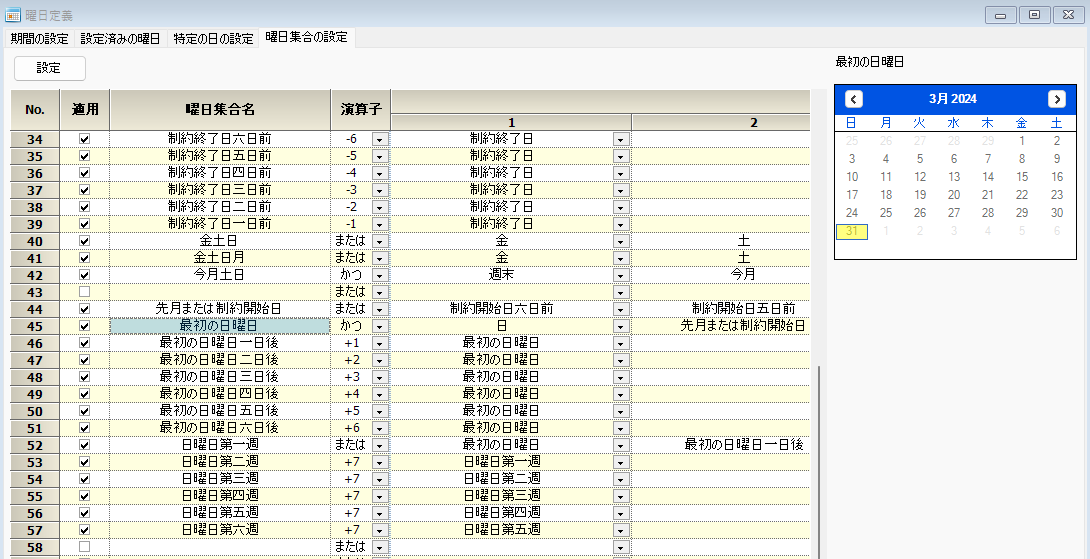
日曜日の第一週集合です。
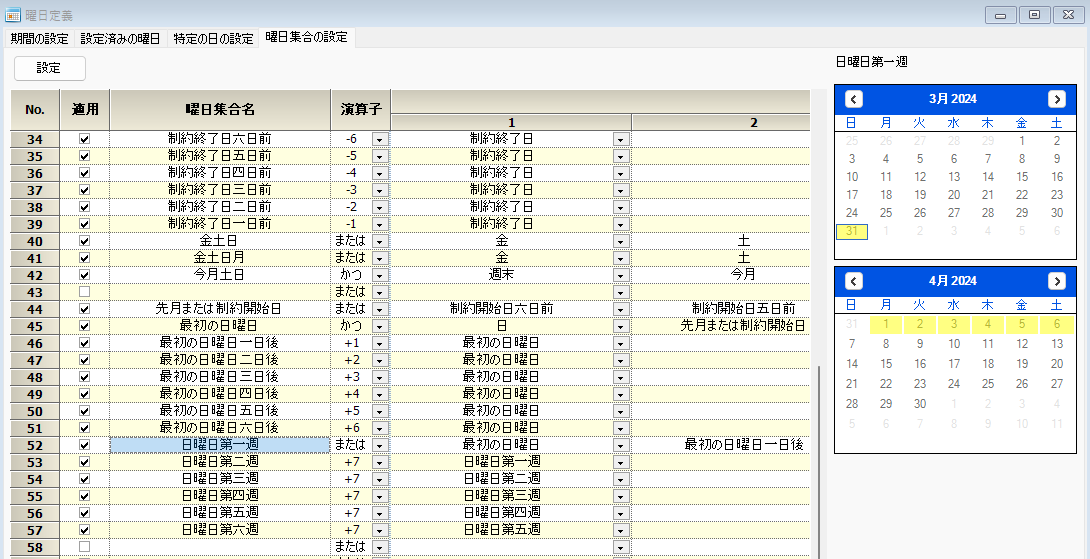
同様にして第2週も定義できます。
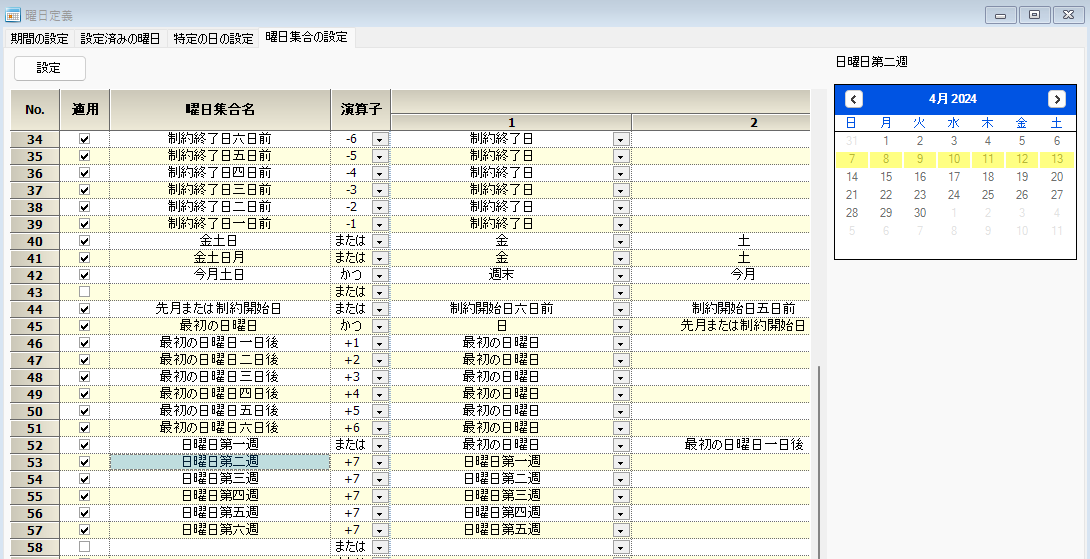
第5週の定義です。月によっては第6週まで必要です。
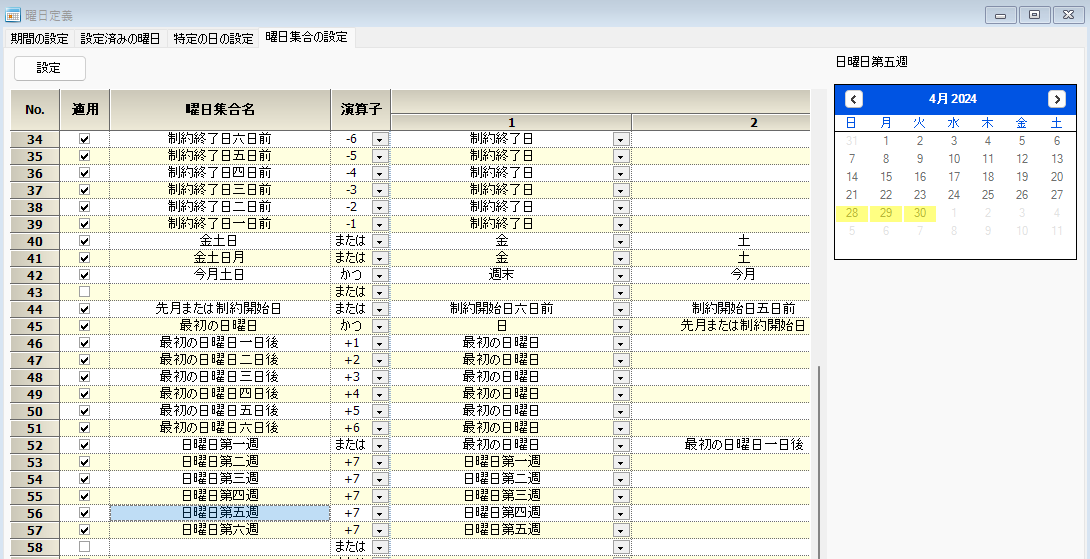
これで、必要な曜日集合が定義できました。
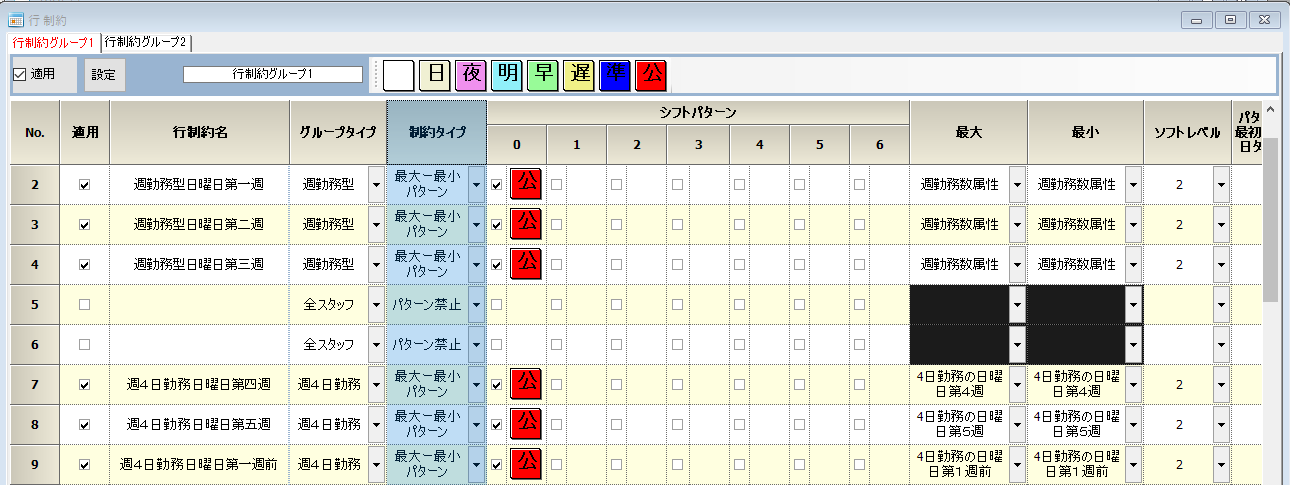
定義した集合を用いて制約します。
端数の処理
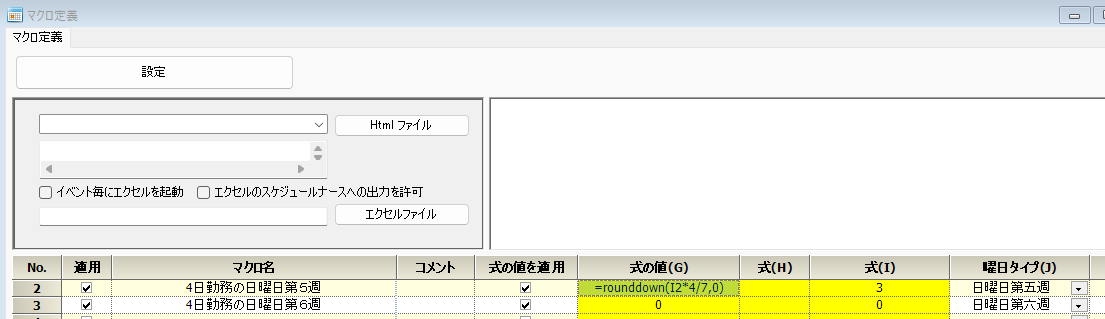
第5・第6週は、端数になる可能性があります。そのためマクロを定義します。
次は、マクロの値をマウスホイールボタンを押して確認しました。第5週の値は、1になっていることが分かります。ちゃんと端数処理されていることが分かります。(第6週の値は0になっていました。)
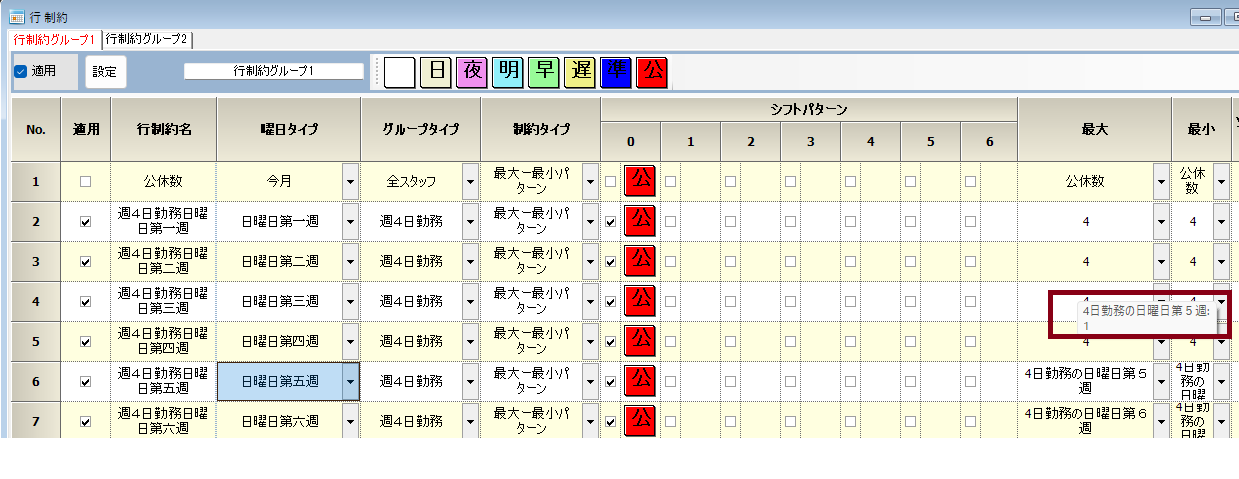
マクロの記述です。
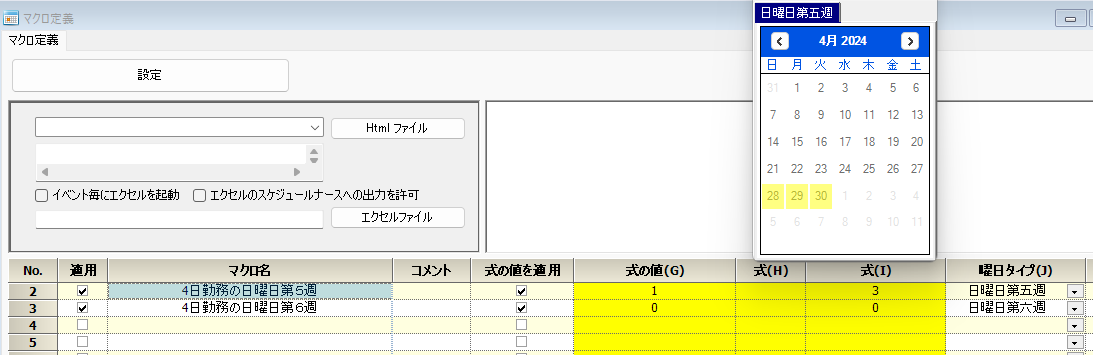
式の中身です。
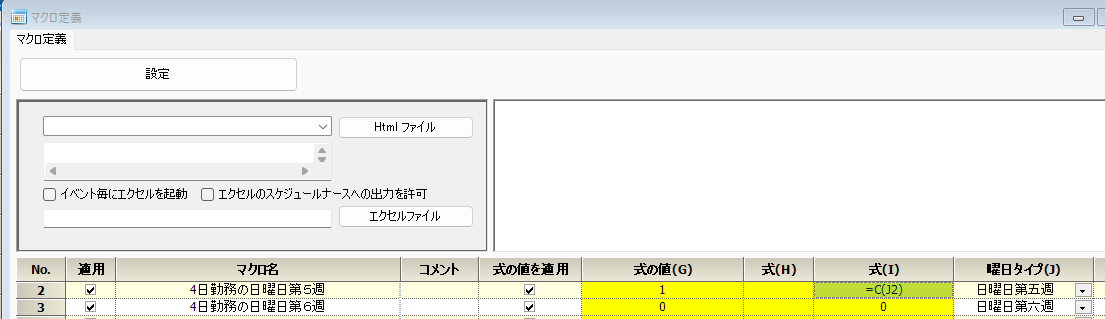
Cは、集合要素を数える関数です。
切り捨て処理を0桁目で行う処理です。rounddown(X,1)だと小数点第一まで出ますが整数でしか処理できないので、0を指定しています。
rounddown/roundupが正しい切り捨て、切り上げ処理になります。
同様にして、週3日、週2日についても記述します。
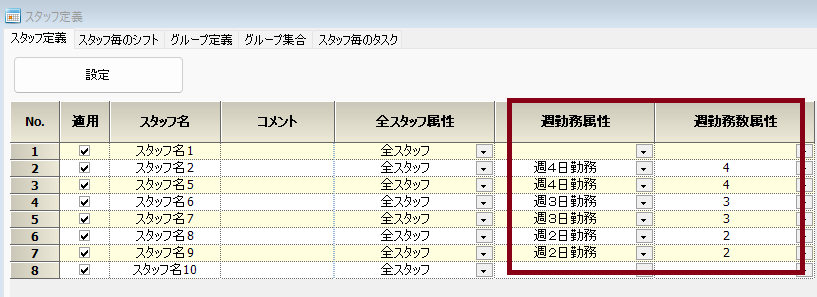
スタッフプロパティ
あまり美しくないです。
先月分を見ない実装
先月部は、見ません。先月分には依存しない実装です。
逆に言えば、先月部からの1週間を見て、目標値に対する制約をすることが出来ません。
上の実装は、先月部を含めて一週間を見るので、先月の切り捨て処理が仮に不正確だったとしても、先月から見て1週間で制約しており補正する力が働きます。
が、今回の実装では、それがないことに注意してください。
今月第一週の存在する日曜を起点として定義します。
そして、日曜日第一週前がポイントとなる集合です。
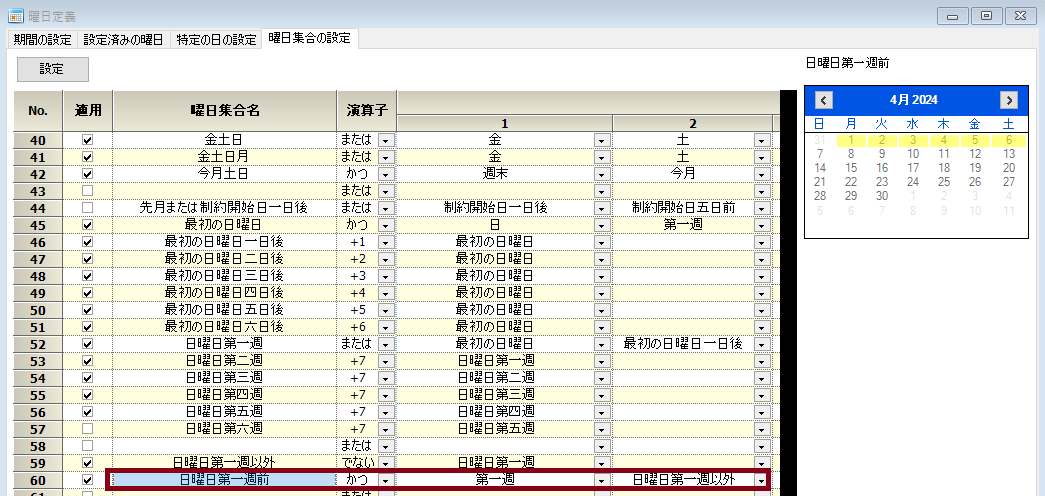
この集合に対しては、先月部切り捨て処理したことを前提に残りの勤務数を割り当てる必要があるので、マクロも別に演算する必要があります。



第一週~第三週が通常処理、それ以外マクロを使います。
解
プロジェクト
プロジェクトは、以下です。
ダウンロード
して、実装の参考にしてください。
先月6日用
先月を見ない実装